Relasi dan Fungsi : Pengertian, Jenis dan Soal-soal Latihan

 

Pengertian Relasi

           Relasi adalah hubungan antara himpunan dari daerah asal (domain) dan daerah kawan (kodomain). Anggota himpunan dari daerah asal dipasangkan dengan anggota himpunan dari daerah kawan sesuai dengan relasinya. 

        Perhatikan contoh berikut :

        A = {Tokyo, Bangkok, Seoul}

        B = {Thailand, Korea Selatan, Jepang}

        C = {kimchi, pad thai, bulgogi, sushi}

        Relasi antara himpunan A dan B

        R : A -> B = {(Tokyo, Jepang), (Bangkok, Thailand), (Seoul, Korea Selatan)}

Setiap anggota himpunan A tepat berpasangan dengan setiap satu anggota himpunan B, sehingga relasinya disebut sebagai fungsi atau lebih spesifiknya korespondensi satu-satu.

        Relasi antara himpunan C dan B

        B = {Thailand, Korea Selatan, Jepang}

        C = {kimchi, pad thai, bulgogi, sushi}

        R : B -> C = {(Thailand, pad thai), (Korea Selatan, kimchi), (Korea Selatan, bulgogi), 

                            (Jepang, sushi)}

Hubungan di atas bukanlah fungsi karena ada satu anggota himpunan B yang berpasangan dengan 2 anggota himpunan C, yaitu Korea Selatan yang berpasangan dengan kimchi dan bulgogi. Namun, keduanya masih termasuk relasi.

Contoh relasi dalam kehidupan sehari-hari juga bisa kamu lihat pada silsilah keluarga di mana setiap orangtua bisa memiliki anak lebih dari satu.

Cara Menyatakan Relasi

1. Diagram panah

        Cara menyatakannya adalah dengan membuat dua bangun yang merepresentasikan domain dan kodomain. Di dalam bangun tersebut diberi tanda berupa titik sebanyak anggota himpunannya. Lalu, hubungkan titik-titik dari daerah domain menuju titik-titik daerah kodomain menggunakan tanda panah.

Contoh 1

A = {1, 2, 3, 4}

B = {1, 4, 9, 16, 25}

Tuliskan dahulu domain serta kodomainnya.

Domain: A = {1, 2, 3, 4}

Kodomain: B = {1, 4, 9, 16, 25}

Relasi: A akar dari B

Model: R: √x -> x²

Bentuk diagram panahnya adalah sebagai berikut.

Daerah hasil atau biasa disebut range = {1, 4, 9, 16}. Untuk 25 tidak termasuk hasil karena tidak memiliki pasangan dari daerah domain.

Contoh 2

P = {2, 3, 4, 5}

Q = {4, 7, 8, 9, 10}

Tuliskan dahulu domain dan kodomainnya.

Domain: P = {2, 3, 4, 5}

Kodomain: Q = {4, 7, 8, 9, 10}

Relasi: A faktor dari B

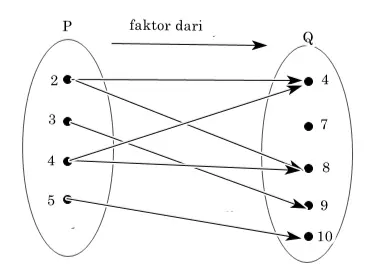
Coba  perhatikan dua contoh diagram panah di atas. Adakah perbedaan antara keduanya?

• Pada contoh 1, setiap anggota domain tepat berpasangan dengan satu anggota kodomain secara berurutan. Dengan demikian, diagram panah tersebut menunjukkan suatu relasi yang disebut himpunan pasangan berurutan.
• Sementara itu, pada contoh 2 satu anggota domain ada yang berpasangan dengan dua anggota kodomain. Artinya, diagram panah tersebut hanya disebut relasi.

2. Diagram Cartesius

        Selain diagram panah, relasi juga bisa ditulis dalam bentuk diagram Cartesius. Sumbu X menunjukkan daerah domain dan sumbu Y nya daerah kodomain. 

Perhatikan contoh berikut.

A = {1, 2, 3, 4}

B = {1, 4, 9, 16, 25}

Tuliskan dahulu domain serta kodomainnya.

Domain: A = {2, 3, 4, 5, 6}

Kodomain: B = {1, 2, 3, 4}

Relasi: R: x -> x + 1

Diagram Cartesisunya digambarkan seperti berikut.

 

 Pengertian Fungsi (Pemetaan)

        Fungsi adalah hubungan antara daerah domain dan kodomian, di mana setiap satu anggota domain tepat berpasangan dengan satu anggota kodomain. fungsi merupakan bentuk relasi khusus. Setiap fungsi sudah bisa dipastikan relasi. Namun, setiap relasi belum tentu fungsi. 

        Adapun syarat khusus yang harus dipenuhi suatu relasi agar bisa dikatakan fungsi.

• Tidak boleh ada anggota domain yang tidak berpasangan. Artinya, seluruh anggota domain harus memiliki pasangan.
• Tidak boleh ada anggota domain yang berpasangan lebih dari satu atau bercabang.

Jenis-jenis Fungsi

#1. Fungsi injektif

       Fungsi injektif disebut juga fungsi satu-satu. Fungsi $f:A\to B$

dikatakan fungsi injektif jika dan hanya jika anggota kodomain dipasangkan satu kali dengan anggota domain. Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, tapi semua anggota kodomain yang terpasangkan hanya ada satu, tidak boleh ada yang lebih dari satu. Perhatikan gambar berikut.

#2. Fungsi surjektif

        Fungsi surjektif yaitu fungsi yang memiliki ciri bahwa anggota kodomainnya boleh memiliki pasangan lebih dari satu, tapi tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih banyak dari anggota domain. Untuk lebih jelasnya, perhatikan gambar berikut.

#3. Fungsi bijektif

        Fungsi bijektif merupakan gabungan dari fungsi injektif dan fungsi surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan. Perhatikan gambar di bawah. Perhatikan gambar berikut.

Notasi Fungsi

        Penulisan fungsi sama seperti relasi, misalnya notasi dari fungsi A ke B bisa dinyatakan sebagai f: A -> B, f(a) = b. Notasi tersebut memiliki arti fungsi f memetakan setiap anggota himpunan A dengan satu anggota himpunan B.

 SOAL - SOAL LATIHAN

Contoh Soal 1

Sebuah fungsi f: x -> y dengan  f(x) = 4 + 2x memiliki daerah asal {1, 3, 5, 7}. Gambarkan diagram panah fungsi tersebut.

Pembahasan:

Pertama, tentukan dahulu daerah kawan (kodomain) yang anggotanya sama dengan daerah hasil. Caranya adalah dengan mensubstitusikan nilai daerah asal pada persamaan fungsi yang tersedia.

Dengan demikian, daerah hasilnya adalah {6, 10, 14, 18}

Jika digambarkan dalam bentuk diagram panah, menjadi seperti berikut.

Contoh Soal 2

Pak Hasan memiliki himpunan S, T, U, V, dan W yang masing-masing anggotanya adalah sebagai berikut.

• S = {(3,2), (4,3), (5,7), (6,8)}
• T = {(2,3), (2,4), (3,5), (4,7)}
• U = {(1,3), (2,3), (3,5),(4,9)}
• V = {(4,5), (1,2), (3,9), (7,10)}
• W = {(1,2), (1,3), (2,3), (2,4)}

Tentukan jenis himpunan yang dimiliki Pak Hasan tersebut!

Pembahasan:

Himpunan S = {(3,2), (4,3), (5,7), (6,8)}

Domain = {3, 4, 5, 7}

Kodomain = {2, 3, 7, 8}

Jika diperhatikan, setiap anggota himpunan domain tepat berpasangan dengan satu anggota himpunan kodomain. 

Tidak hanya itu, setiap satu anggota kodomain hanya memiliki satu pasang anggota domain. 

Artinya, himpunan S merupakan fungsi bijektif atau korespondensi satu-satu.

Himpunan T = {(2,3), (2,4), (3,5), (4,7)}

Domain = {2, 3, 4}

Kodomain = {3, 4, 5, 7}

Jika diperhatikan, ada satu anggota domain yang berpasangan dengan dua anggota kodomain, yaitu (2,3) dan (2,4). 

Artinya, himpunan T merupakan relasi atau tidak termasuk fungsi.

Himpunan U = {(1,3), (2,3), (3,5), (4,9)}

Domain = {1, 2, 3, 4}

Kodomain = {3, 5, 9}

Jika diperhatikan, setiap satu anggota domain berpasangan dengan tepat satu anggota kodomain. 

Namun, ada anggota kodomain yang berpasangan dengan dua anggota domain. Artinya, himpunan U merupakan fungsi surjektif.

Himpunan V = {(4,5), (1,2), (3,9), (7,10)}

Domain = {4, 1, 3, 7}

Kodomain = {5, 2, 9, 10}

Jika diperhatikan, setiap anggota himpunan domain tepat berpasangan dengan satu anggota himpunan kodomain. 

Tidak hanya itu, setiap satu anggota kodomain hanya memiliki satu pasang anggota domain. 

Artinya, himpunan V merupakan fungsi bijektif atau korespondensi satu-satu.

Himpunan W = {(1,2), (1,3), (2,3), (2,4)}

Domain = {1, 2}

Kodomain = { 2, 3, 4}

Jika diperhatikan, satu anggota domain berpasangan dengan lebih dari satu anggota kodomain. 

Artinya, himpunan W merupakan relasi atau tidak termasuk fungsi.

Jadi, himpunan S = fungsi bijektif, himpunan T = relasi, himpunan U = fungsi surjektif, himpunan V = fungsi bijektif, dan himpunan W = relasi.

 

CONTOH SOAL 3

 

 CONTOH SOAL 4

CONTOH SOAL 5

 

CONTOH SOAL 6

CONTOH SOAL 7

Sebuah pemetaan dinytakan dalam bentuk R = {(1,a), (2,b), (3,a), (4,b)}. Tentukan domain, kodomain dan rangenya…

Jawaban:

R = {(1,a), (2,b), (3,a), (4,b)}.

Dari R kita peroleh:

Domain = {1,2,3,4)

Kodomain = {a,b}

Range = {a,b}

CONTOH SOAL 8

Diketahui M={2, 3, 4, 5, 6} dan N={a,b}. Relasi R memasangkan setiap bilangan genap pada M dengan a dan setiap bilangan ganjil pada M dengan b.

a. Nyatakan R dengan diagram panah

b. Apakah R merupakan pemetaan dari M ke N

Jawaban:

a. Nyatakan R dengan diagram panah

M={2, 3, 4, 5, 6}

N={a, b}

b. Apakah R merupakan pemetaan dari M ke N

Ya, R merupakan pemetaan dari M ke N. Karena masing-masing anggota M memiliki tepat satu pasangan di N.

CONTOH SOAL 9

Diketahui  A = {bilangan ganjil kurang dari 8} dan B = {bilangan prima genap}.  Banyak pemetaan dari B ke A adalah…

Jawaban:

A = {bilangan ganjil kurang dari 8}

A = {1,3,5,7}

n(A) = 4

B = {bilangan prima genap}

B = {2}

n(B) = 1

Banyak pemetaan dari B ke A = 4¹ = 4

CONTOH SOAL 10

Berapakah banyak pemetaan yang mungkin terjadi dari himpunan M = {p, q, r} ke himpunan N = {1, 2, 3, 4}. 

Jawaban:

Untuk mengetahui banyaknya pemetaan yang mungkin terjadi, kita dapat menggunakan rumus berdasarkan banyak anggota domain dan banyak anggota kodomain.

Pada soal:

M = {p, q,  r}

N = {1, 2, 3, 4}.

Banyak anggota himpunan M = n(M) = 3

Banyak anggota himpunan N = n(N) = 4

Banyak pemetaan dari M ke N = 4³ = 64 cara

 

CONTOH SOAL 11

1. Buatlah tabel fungsi f : x → x + 1 dari himpunan {0, 1, 2, 3} ke himpunan bilangan bulat.

2. Gambarlah grafik fungsi f tersebut.

3. Pada gambar yang sama, gambarlah grafik fungsi x → x + 1 pada himpunan semua bilangan positif dan nol.

Jawaban:

1. f : x → x + 1 dari himpunan {0, 1, 2, 3} ke himpunan bilangan bulat.

2. Gambarlah grafik fungsi f

3. Pada gambar yang sama, gambarlah grafik fungsi x → x + 1 pada himpunan semua bilangan positif dan nol.

CONTOH SOAL 12

Diketahui fungsi f:x → (2m + 1)x + 7. Jika f(-1) = -4, maka nilai f(m) sama dengan…

Jawaban:

f : x → (2m + 1)x + 7

f (-1) = -4

(2m + 1)(-1) + 7 = -4

-2m – 1 + 7 = -4

-2m + 6 = -4

-2m = -10

m = 5

Karena x = -1, m = 5 maka f(m) yaitu:

f(m) = (2 x 5 + 1)(-1) + 7

= 11(-1) + 7 = -11+7 = -4

CONTOH SOAL 13

Fungsi f : x→2x + 3. Jika nilai f(a) = 17, maka nilai dari a adalah…

Jawaban:

f : x→2x + 3

f(a) = 17

2a + 3 = 17

2a = 14

a = 7

Jadi, nilai dari a adalah 7.

CONTOH SOAL 14

Pada pemetaan f:x→ax+b, jika f(2) = 1 dan f(7) = 16 maka a –b adalah…

Jawaban:

f:x→ax+b

f(2) = 1

2a + b = 1 

b = 1 -2a

f(7) = 16

7a + b = 16 (persamaan 1)

Substitusikan b = 1 – 2a ke dalam persamaan 1.

7a + b = 16

7a + (1 – 2a) = 16

7a + 1 – 2a = 16

5a + 1 = 16

5a = 15

a = 3

Karena kita telah peroleh a = 3 maka kita akan mencari nilai b dengan mensubstitusikannya ke dalam b = 1 – 2a sebagai berikut.

b = 1 – 2a

b = 1 – 2(3) = 1 – 6 = -5

Dengan demikian,

a –b = 3 – (-5) = 8

CONTOH SOAL 15

Empat orang anak bernama Erwin, Anggi, Dinda, dan Adam. Erwin berbadan tinggi, sedangkan anak yang lain tidak. Dinda berambut keriting, anak yang lain tidak. Anggi, Dinda dan Adam berkulit kuning, anak yang lain tidak.

a. Buatlah diagram panah yang menghubungkan setiap anak dengan sifatnya.

b. Siapakah yang berbadan tinggi dan berkulit kuning?

c. Siapakah yang berkulit kuning tetapi tidak berambut keriting?

Jawaban:

a. Buatlah diagram panah yang menghubungkan setiap anak dengan sifatnya

Empat orang anak bernama Erwin, Anggi, Dinda, dan Adam sebagai domain. 

Tinggi, keriting dan kuning sebagai kodomain.

Diagram panah-nya akan seperti berikut.

b. Anak yang berbadan tinggi dan berkulit kuning adalah Anggi.

c. Anak yang berkulit kuning tetapi tidak berambut keriting adalah Anggi dan Adam.

 

 

CONTOH SOAL 16

 

CONTOH SOAL 17

CONTOH SOAL 18

Semua siswa SD Sukamaju mendapatkan nomor bangku ujian. Tidak ada satupun siswa yang memiliki nomor bangku sama. Relasi antara siswa dan nomor bangkunya termasuk dalam fungsi ….

1. Surjektif
2. Relasi
3. Injeksi
4. Bijektif

Pembahasan:

Semua siswa SD Sukamaju mendapatkan nomor bangku ujian yang berbeda. Artinya, tidak akan ada anak yang memiliki nomor bangku sama. Jika dinyatakan dalam bentuk relasi, anggota asal/ domain (anak) tepat berpasangan satu-satu dengan anggota kawan/ kodomain (nomor bangku). Relasi semacam ini disebut sebagai korespondensi satu-satu atau fungsi bijektif.

Jadi, relasi antara siswa dan nomor bangkunya termasuk dalam fungsi bijektif.

Jawaban: D

CONTOH SOAL 19

Sebuah tempat wisata memasang tarif masuk Rp10.000 setiap orang dan ditambah tarif parkir Rp5.000 untuk setiap kendaraan roda empat. Jika Ani datang ke tempat wisata tersebut bersama 3 rekannya menggunakan mobil, biaya yang harus ia bayarkan adalah ….

1. Rp35.000
2. Rp40.000
3. Rp 45.000
   
4. Rp50.000

Pembahasan:

Diketahui:

Tarif parkir = Rp.5000

Tarif masuk = Rp10.000/orang

Secara keseluruhan, tarif masuk tempat wisata dengan roda empat dinyatakan sebagai berikut.

f (x) = 10.000x + 5.000

Jika Ani dan tiga rekannya (4 orang) masuk, uang yang harus dibayarkan adalah sebagai berikut.

f (x) = 10.000x + 5.000

       = 10.000(4) + 5.000

       = 40.000 + 5.000

       = 45.000

Jadi, biaya yang harus dibayarkan Ani adalah Rp45.000.

Jawaban: C

CONTOH SOAL 20

Farel melemparkan bola dari rooftop rumahnya. Gerak bola tersebut mengikuti persamaan f(t) = 10 – 2t dengan t dalam s. Waktu yang diperlukan bola untuk sampai tanah adalah ….

1. 5 s
2. 6 s
3. 4 s
4. 3 s

Pembahasan:

Diketahui:

Farel melemparkan bola dari rooftop rumahnya. Gerak bola tersebut mengikuti persamaan f(t) = 10 – 2t.

Ditanya: t = …?

Jawab:

Waktu yang dibutuhkan bola untuk sampai tanah yang ketinggiannya 0 m dirumuskan sebagai berikut.

f(t) = 10 – 2t

↔ 0 = 10 – 2t

↔2t = 10

↔t = 5 s

Jadi, waktu yang dibutuhkan bola untuk sampai tanah adalah 5 s.

Jawaban: A